OpenGL ES from the Ground Up 9 (intermission): Quaternions

Before we can get into the next post in the OpenGL ES from the Ground Up, which covers skeletal animation, we have to take a little detour and talk about a new datatype we'll be using, the Quaternion. We'll use quaternions to store the rotation on all three axes of a single bone or, in other words, to store the direction the bone is pointing. In skeletal animation, as you'll see in the next installment, vertices in the model are attached to one or more bones and move as the bones they are attached to move. Using quaternions, as opposed to storing the three Euler angles of in three GLfloats or a single Vector3D has two advantages:

1. Quaternions are not subject to gimbal lock. Euler angles are, so quaternions will allow our 3D skeletons to have full range of motion.
2. Combining multiple rotations using quaternions requires significantly less calculations than doing matrix rotate transformations for each Euler angle

Now, quaternions are horribly complex and difficult to understand. They are advanced mathematics: completely crazy juju. Fortunately, you do not need to fully understand the underlying math to use them. But, we need to use quaternions to accomplish skeletal animation, so it's worth a second to talk about what they are and how we use them.

Discovery

Mathematically speaking, quaternions are an extension of complex numbers and were discovered by Sir William Rowan Hamilton in 1843. Technically speaking, quaternions form a "four-dimensional normed division algebra over the real numbers". Zoiks! More simply, a quaternion uses a fourth dimension to allow the calculation of triples for all three Cartesian coordinates by providing each axis with three other values. Okay, maybe that wasn't all that simple, was it?

Don't get scared off yet. If you're not deeply-versed in advanced mathematics, quaternions can make your brain hurt. But, as I said earlier, you really don't have to grok Quaternions to use them. The concept is very similar to something you've already seen. If you recall, matrix transformations involve the use of a 4x4 matrix to apply transformations in three dimensional space. When it comes time to use the transformed data, we just ignore the fourth value. Think of the fourth value in a quaternion as a work value, it's just there to provide a space for the calculations. Math majors, please don't yell at me - this oversimplification will help mere mortals live at peace with quaternions.

Quaternions were considered rather revolutionary at the time of discovery, but their heyday was somewhat short-lived. In the mid-1880s, vector calculus began to supplant quaternion theory in mathematics, since it described the same phenomena using concepts that are easier to understand and describe.

Not Quite Dead Yet!

In the 20th century, however, quaternions came back into favor. As we discussed in part 7, there is a phenomenon called gimbal lock that can occur when you do rotation transformations individually on each axis, which has the undesirable effect of stopping rotation on one of the three axes.

Despite the fact that quaternions came out of complex, theoretical mathematics, they do have practical applications. One such practical application is the representation of angles of rotation on all three axes. Because quaternions represent the Cartesian (or three-axis) rotation using four dimensions, the representation is not subject to gimbal lock, and you can convert between quaternions and rotation matrices as well as between quaternions and Euler angles with no loss of fidelity¹. This makes them absolutely perfect for storing rotation information about an object, like say… an individual bone of an articulated skeleton? Instead of storing the angle on three axes, we store a single quaternion.

Quaternions can be multiplied like matrices, and rotation values stored in different quaternions can be combined by multiplying them. The result of a quaternion multiplication is exactly the same as matrix multiplication with two rotation matrices, and involves considerably less calculations to accomplish, meaning that in addition to avoiding gimbal lock, we reduce the number of FLOPS we perform each time through our application loop. Not only are there less operations in quaternion multiplication than matrix multiplication, but since we also can represent all three axes using a single quaternion, we typically can do less quaternion multiplications than matrix multiplications. If we were storing rotation in a Vector3D or using three GLfloats, we would often have to do three matrix multiplications — one for each axis. As a result, storing quaternions can lead to a substantial performance improvement over storing individual angles of rotation.

The Quaternion Struct

From a data standpoint, a Quaternion is nothing more than a Vector3D with an additional GLfloat, usually referred to as w. So, for our purposes, a quaternion will look like this:

typedef struct {
   GLfloat x;
   GLfloat y;
   GLfloat z;
   GLfloat w;
} Quaternion3D;

Normalizing a Quaternion

Easy enough. Now, just like Vector3Ds, since quaternions represent a direction in space, the actual distance values don't matter, and it's common to normalize them down to 1.0 before and/or after doing other calculations. We can accomplish that like so:

static inline void Quaternion3DNormalize(Quaternion3D *quaternion)
{
   GLfloat magnitude;
  
   magnitude = sqrtf((quaternion->x * quaternion->x) +
                     (quaternion->y * quaternion->y) +
                     (quaternion->z * quaternion->z) +
                     (quaternion->w * quaternion->w));
  
   quaternion->x /= magnitude;
   quaternion->y /= magnitude;
   quaternion->z /= magnitude;
   quaternion->w /= magnitude;
}

Creating a Quaternion from a Rotation matrix

Quaternions don't do us any good if we don't have any way of converting quaternions to and from our other objects used to represent angles of rotation. Let's first look at creating a quaternion from a rotation matrix. Here's what the function to do it looks like:

static inline Quaternion3D Quaternion3DMakeWithMatrix3D(Matrix3D matrix)
{
   Quaternion3D quat;
   GLfloat trace, s;
  
   trace = matrix[0] + matrix[5] + matrix[10];
   if (trace > 0.0f)
   {
       s = sqrtf(trace + 1.0f);
       quat.w = s * 0.5f;
       s = 0.5f / s;
      
       quat.x = (matrix[9] - matrix[6]) * s;
       quat.y = (matrix[2] - matrix[8]) * s;
       quat.z = (matrix[4] - matrix[1]) * s;
   }
   else
   {
       NSInteger biggest;
       enum      {A,E,I};
       if (matrix[0] > matrix[5])
           if (matrix[10] > matrix[0])
               biggest = I;   
           else
               biggest = A;
       else
           if (matrix[10] > matrix[0])
               biggest = I;
           else
               biggest = E;
      
       switch (biggest)
       {
           case A:
               s = sqrtf(matrix[0] - (matrix[5] + matrix[10]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.x = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[9] - matrix[6]) * s;
                   quat.y = (matrix[1] + matrix[4]) * s;
                   quat.z = (matrix[2] + matrix[8]) * s;
                   break;
               }
               s = sqrtf(matrix[10] - (matrix[0] + matrix[5]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.z = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[4] - matrix[1]) * s;
                   quat.x = (matrix[8] + matrix[2]) * s;
                   quat.y = (matrix[9] + matrix[6]) * s;
                   break;
               }
               s = sqrtf(matrix[5] - (matrix[10] + matrix[0]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.y = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[2] - matrix[8]) * s;
                   quat.z = (matrix[6] + matrix[9]) * s;
                   quat.x = (matrix[4] + matrix[1]) * s;
                   break;
               }
               break;
              
           case E:
               s = sqrtf(matrix[5] - (matrix[10] + matrix[0]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.y = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[2] - matrix[8]) * s;
                   quat.z = (matrix[6] + matrix[9]) * s;
                   quat.x = (matrix[4] + matrix[1]) * s;
                   break;
               }
               s = sqrtf(matrix[10] - (matrix[0] + matrix[5]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.z = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[4] - matrix[1]) * s;
                   quat.x = (matrix[8] + matrix[2]) * s;
                   quat.y = (matrix[9] + matrix[6]) * s;
                   break;
               }
               s = sqrtf(matrix[0] - (matrix[5] + matrix[10]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.x = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[9] - matrix[6]) * s;
                   quat.y = (matrix[1] + matrix[4]) * s;
                   quat.z = (matrix[2] + matrix[8]) * s;
                   break;
               }
               break;
              
           case I:
               s = sqrtf(matrix[10] - (matrix[0] + matrix[5]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.z = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[4] - matrix[1]) * s;
                   quat.x = (matrix[8] + matrix[2]) * s;
                   quat.y = (matrix[9] + matrix[6]) * s;
                   break;
               }
               s = sqrtf(matrix[0] - (matrix[5] + matrix[10]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.x = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[9] - matrix[6]) * s;
                   quat.y = (matrix[1] + matrix[4]) * s;
                   quat.z = (matrix[2] + matrix[8]) * s;
                   break;
               }
               s = sqrtf(matrix[5] - (matrix[10] + matrix[0]) + 1.0f);
               if (s > QUATERNION_TRACE_ZERO_TOLERANCE)
               {
                   quat.y = s * 0.5f;
                   s = 0.5f / s;
                   quat.w = (matrix[2] - matrix[8]) * s;
                   quat.z = (matrix[6] + matrix[9]) * s;
                   quat.x = (matrix[4] + matrix[1]) * s;
                   break;
               }
               break;
              
           default:
               break;
       }
   }
   return quat;
}

Well, ugh! If you really want to understand what's going on here, it's going to require an understanding of matrix calculus, Euler's rotation theorem, and the concepts of eigenvalues and trace, not to mention a thorough understanding of the way rotations are represented in matrices. When you've finished your PhD in mathematics, you can come back and explain it to the rest of usl. You can find the algorithm used in this function laid out in pseudocode at the Matrix FAQ.

Creating a Rotation Matrix from a Quaternion

Going the other way is actually a little bit easier. Again, the basic algorithm comes from the Matrix FAQ, though I had to switch it to row-major ordering:

static inline void Matrix3DSetUsingQuaternion3D(Matrix3D matrix, Quaternion3D quat)
{
   matrix[0]  = (1.0f - (2.0f * ((quat.y * quat.y) + (quat.z * quat.z))));
   matrix[1]  = (2.0f * ((quat.x * quat.y) - (quat.z * quat.w)));
   matrix[2]  = (2.0f * ((quat.x * quat.z) + (quat.y * quat.w)));
   matrix[3] = 0.0f;
   matrix[4]  = (2.0f * ((quat.x * quat.y) + (quat.z * quat.w)));
   matrix[5]  = (1.0f - (2.0f * ((quat.x * quat.x) + (quat.z * quat.z))));
   matrix[6]  = (2.0f * ((quat.y * quat.z) - (quat.x * quat.w)));
   matrix[7] = 0.0f;
   matrix[8]  = (2.0f * ((quat.x * quat.z) - (quat.y * quat.w)));
   matrix[9]  = (2.0f * ((quat.y * quat.z) + (quat.x * quat.w)));
   matrix[10] = (1.0f - (2.0f * ((quat.x * quat.x) + (quat.y * quat.y))));
   matrix[11] = 0.0f;
   matrix[12]  = 0.0f;
   matrix[13]  = 0.0f;
   matrix[14] = 0.0f;
   matrix[15] = 1.0f;
}

Converting an Angle and Axis of Rotation to a Quaternion

Another conversion we can do with quaternions is to rotate on an arbitrary axis represented by a Vector3D. This can be tremendously useful in skeletal animation and is quite difficult to implement using matrices. To create a quaternion based on an angle and axis of rotation, we do this:

static inline Quaternion3D Quaternion3DMakeWithAxisAndAngle(Vector3D axis, GLfloat angle)
{
   Quaternion3D quat;
   GLfloat sinAngle;
  
   angle *= 0.5f;
    Vector3DNormalize(&axis);
   sinAngle = sinf(angle);
   quat.x = (axis.x * sinAngle);
   quat.y = (axis.y * sinAngle);
   quat.z = (axis.z * sinAngle);
   quat.w = cos(angle);
  
   return quat;
}

Extracting an Angle and Axis of Rotation from a Quaternion

We can also go the other way. We can take the rotation represented in a quaternion and extract the angle of rotation and degrees from it, like so:

static inline void Quaternion3DExtractAxisAndAngle(Quaternion3D quat, Vector3D *axis, GLfloat *angle)
{
   GLfloat s;
    Quaternion3DNormalize(&quat);
   s = sqrtf(1.0f - (quat.w * quat.w));
 
   if (fabs(s) < 0.0005f) s = 1.0f;
  
   if (axis != NULL)
   {
       axis->x = (quat.x / s);
       axis->y = (quat.y / s);
       axis->z = (quat.z / s);
   }
  
   if (angle != NULL)
       *angle = (acosf(quat.w) * 2.0f);
}

Quaternion Multiplication

To combine the rotations from two different Quaternion3Ds, we just need to multiply them together. Here we go:

static inline void Quaternion3DMultiply(Quaternion3D *quat1, Quaternion3D *quat2)
{
   Vector3D v1, v2, cp;
   float angle;
  
   v1.x = quat1->x;
   v1.y = quat1->y;
   v1.z = quat1->z;
   v2.x = quat2->x;
   v2.y = quat2->y;
   v2.z = quat2->z;
   angle = (quat1->w * quat2->w) - Vector3DDotProduct(v1, v2);
  
   cp = Vector3DCrossProduct(v1, v2);
   v1.x *= quat2->w;
   v1.y *= quat2->w;
   v1.z *= quat2->w;
   v2.x *= quat1->w;
   v2.y *= quat1->w;
   v2.z *= quat1->w;
  
   quat1->x = v1.x + v2.x + cp.x;
   quat1->y = v1.y + v2.y + cp.y;
   quat1->z = v1.z + v2.z + cp.z;
   quat1->w = angle;
}

Inverting a Quaternion

We can do a spacial invert of a quaternion by conjugating it. Conjugating a quaternion just means that we invert the the three components of the quaternion that represents the vector (x, y, and z). In this implementation, we also normalize the quaternion as part of the calculation rather than as a separate step:

static inline void Quaternion3DInvert(Quaternion3D  *quat)
{
   GLfloat length = 1.0f / ((quat->x * quat->x) +
                    (quat->y * quat->y) +
                    (quat->z * quat->z) +
                    (quat->w * quat->w));
   quat->x *= -length;
   quat->y *= -length;
   quat->z *= -length;
   quat->w *= length;
}

Creating a Quaternion from Euler Angles

I've warned against Euler angles for rotation, but there are times when you'll have to convert Euler angles to a quaternion, such as when accepting input from a user. To do this, we have to create Vector3Ds to represent each of the Euler axes, create Quaternions using those vectors and the passed in values, then use quaternion multiplication to combine the resulting quaternions.

static inline Quaternion3D Quaternion3DMakeWithEulerAngles(GLfloat x, GLfloat y, GLfloat z)
{
   Vector3D vx = Vector3DMake(1.f, 0.f, 0.f);
   Vector3D vy = Vector3DMake(0.f, 1.f, 0.f);
   Vector3D vz = Vector3DMake(0.f, 0.f, 1.f);
  
   Quaternion3D qx = Quaternion3DMakeWithAxisAndAngle(vx, x);
   Quaternion3D qy = Quaternion3DMakeWithAxisAndAngle(vy, y);
   Quaternion3D qz = Quaternion3DMakeWithAxisAndAngle(vz, z);


    Quaternion3DMultiply(&qx, &qy );
    Quaternion3DMultiply(&qx, &qz );
   return qx;
}

SLERPs and NLERPS

Finally, the piece de resistance: SLERPs and NLERPS. SLERP is shorthand for Spherical Linear Interpolation and NLERPS for normalized linear interpolation. Remember how we did algebraic linear interpolation in Part 9a to calculate the correct location for each vertex based on how much time had elapsed? Well, those same calculations are not necessarily going to give us the results we want when interpolating quaternions. Imagine a ball and socket joint: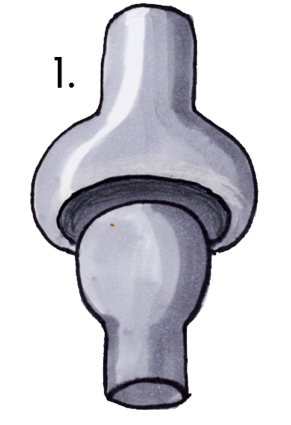

Source: Wikipedia

You know where there's a ball and socket joint? In your shoulder. The clavicle and spine of the scapula form a cradle for the ball shaped protrusion at the top of the humerus bone. Well, that's handy. Stand in front of a mirror, hold your am up over your head, and then keeping your arm straight, bring it down until it's at your side. Your hand doesn't move in a straight line, does it. Your hand moves in an arc and moves faster than your elbow and your shoulder and chances are your hand didn't move at a constant speed. That's the basic movement we want to simulate when we animate angles of rotation.

SLERPs and NLERPs are the two most common approaches. SLERPs are more precise and give a better simulation of reality, but they are slower and more processor intensive. NLERPs are much faster because they are essentially the same linear interpolation we've already used, only normalized after doing the interpolation, which you might have been able to guess from the name "normalized linear interpolation".

Use SLERPs when realistic looking animation is more important than speed, NLERPs otherwise. The two methods take the exact same parameters, so switching between the two shouldn't be a big deal, so you can experiment to see whether SLERPs are worth the additional processing cost.

Here's the simpler NLERP implementation:

static inline Quaternion3D Quaternion3DMakeWithNLERP(Quaternion3D *start, Quaternion3D *finish, GLclampf progress)
{
   Quaternion3D ret;
   GLfloat inverseProgress = 1.0f - progress;
   ret.x = (start->x * inverseProgress) + (finish->x * progress);    
   ret.y = (start->y * inverseProgress) + (finish->y * progress);
   ret.z = (start->z * inverseProgress) + (finish->z * progress);
   ret.w = (start->w * inverseProgress) + (finish->w * progress);
    Quaternion3DNormalize(&ret);
   return ret;
}

Now, the SLERP implementation is a little more complex and requires the ability to calculate a dot product on a Quaternion, which is done exactly the same as calculating the dot product of a vector:

static inline Quaternion3D Quaternion3DMakeWithSLERP(Quaternion3D *start, Quaternion3D *finish, GLclampf progress)
{
   GLfloat startWeight, finishWeight, difference;
   Quaternion3D ret;
  
   difference = ((start->x * finish->x) + (start->y * finish->y) + (start->z * finish->z) + (start->w * finish->w));
   if ((1.f - fabs(difference)) > .01f)
   {
       GLfloat theta, oneOverSinTheta;
      
       theta = acosf(fabsf(difference));
       oneOverSinTheta = (1.f / sinf(theta));
       startWeight = (sinf(theta * (1.f - progress)) * oneOverSinTheta);
       finishWeight = (sinf(theta * progress) * oneOverSinTheta);
       if (difference < 0.f)
           startWeight = -startWeight;
   } else
   {
       startWeight = (1.f - progress);
       finishWeight = progress;
   }
   ret.x = (start->x * startWeight) + (finish->x * finishWeight);
   ret.y = (start->y * startWeight) + (finish->y * finishWeight);
   ret.z = (start->z * startWeight) + (finish->z * finishWeight);
   ret.w = (start->w * startWeight) + (finish->w * finishWeight);
    Quaternion3DNormalize(&ret);
  
   return ret;
}

Finish Line

Okay, now we're armed and dangerous and ready to do some skeletal animation. I'll meet you back here next time for it. I've updated the Xcode project template with these new functions and datatypes.

---

1 Because our programs use floating point variables, we will actually see slight changes in data due to the phenomenon known as loss of significance. This is not because we're using quaternions. It's because we use floating point variables.

Posted in: OpenGL ES,tutorials